With the recent releases of R 3.2.4 and OpenBLAS 2.17, I decided it was time to re-benchmark R speed. I’ve settled on a particular set of tests, based on my experience as well as some of Simon Urbanek’s work which I separated into two groups: those focusing on BLAS-heavy operations and those which do not. I’ve posted the code I use to its own page, but I’ll copy it below for convenience:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
set.seed(4987) library(microbenchmark) library(Matrix) A <- matrix(rnorm(1e6, 1e3, 1e2), ncol = 1e3) B <- matrix(rnorm(1e6, 1e3, 1e2), ncol = 1e3) A <- crossprod(A, A) A <- A * 1000 / mean(A) colnames(A) <- colnames(B) <- NULL options(scipen=4, digits = 3) BLAS <- microbenchmark( sort(c(as.vector(A), as.vector(B))), det(A), A %*% B, t(A) %*% B, crossprod(A, B), solve(A), solve(A, t(B)), solve(B), chol(A), chol(B, pivot = TRUE), qr(A, LAPACK = TRUE), svd(A), eigen(A, symmetric = TRUE), eigen(A, symmetric = FALSE), eigen(B, symmetric = FALSE), lu(A), fft(A), Hilbert(3000), toeplitz(A[1:500, 1]), princomp(A), times=25L, unit='ms', control = list(order = 'block') ) NotBLAS <- microbenchmark( A + 2, A - 2, A * 2, A / 2, A * 0.5, A ^ 2, sqrt(A[1:10000]), sin(A[1:10000]), A + B, A - B, A * B, A / B, A[1:1e5] %% B[1:1e5], A[1:1e5] %/% B[1:1e5], times = 5000L, unit='ms', control = list(order = 'block') ) |
My machine is a i7-2600K overclocked to 4.65Ghz with 16GB RAM, running Win7 64. I’ve also used RStudio Version 0.99.893 for each of these tests.
I ran the tests on four versions of R:
- Plain vanilla R version 3.2.4 Revised (2016-03-16 r70336) installed from the binary on CRAN
- The same version of R as #1, but with Rblas.dll replaced by one based on OpenBLAS 2.17 compiled specifically for the SandyBridge CPU (as part of the #3)
- R compiled from source using the gcc 4.9.3 toolchain, passing
-march=nativeto EOPTS and linking to a multi-threaded (4 max) SandyBridge-specific OpenBLAS 2.17 - Same as #3, but activating link-time optimization for core R and the BLAS
This time I was a bit wiser, and saved the results to RDS objects so that I could combine them into one R session and compare them. I’ll post the raw output at the bottom of the page, but I think it’s more intuitive to look at graphical comparisons. The takeaway is if you can install a fast BLAS! The other optimization options had minor effects, sometimes better sometimes worse, but using a fast BLAS made a significant difference. Adding a Platform variable to the four sets of BLAS and NotBLAS outputs and then combining them in one session allowed for the generation of comparison plots. The call for these graphs, for those following along at home, is:
|
1 2 3 |
ggplot(BLAS) + geom_boxplot(aes(y = time / 1e6, color = Platform, x = expr)) + scale_y_continuous(labels = comma) + ylab('milliseconds') + coord_flip() ggplot(BLAS) + geom_jitter(aes(y = time / 1e6, color = Platform, x = expr), alpha = 0.3) + scale_y_continuous(labels = comma) + ylab('milliseconds') + coord_flip() ggplot(NotBLAS) + geom_boxplot(aes(y = time / 1e6, color = Platform, x = expr)) + scale_y_continuous(labels = comma) + ylab('milliseconds') + coord_flip() |
You may also have to right-click and sellect “View Image” to get a better picture. First is a boxplot comparison for the BLAS related functions:
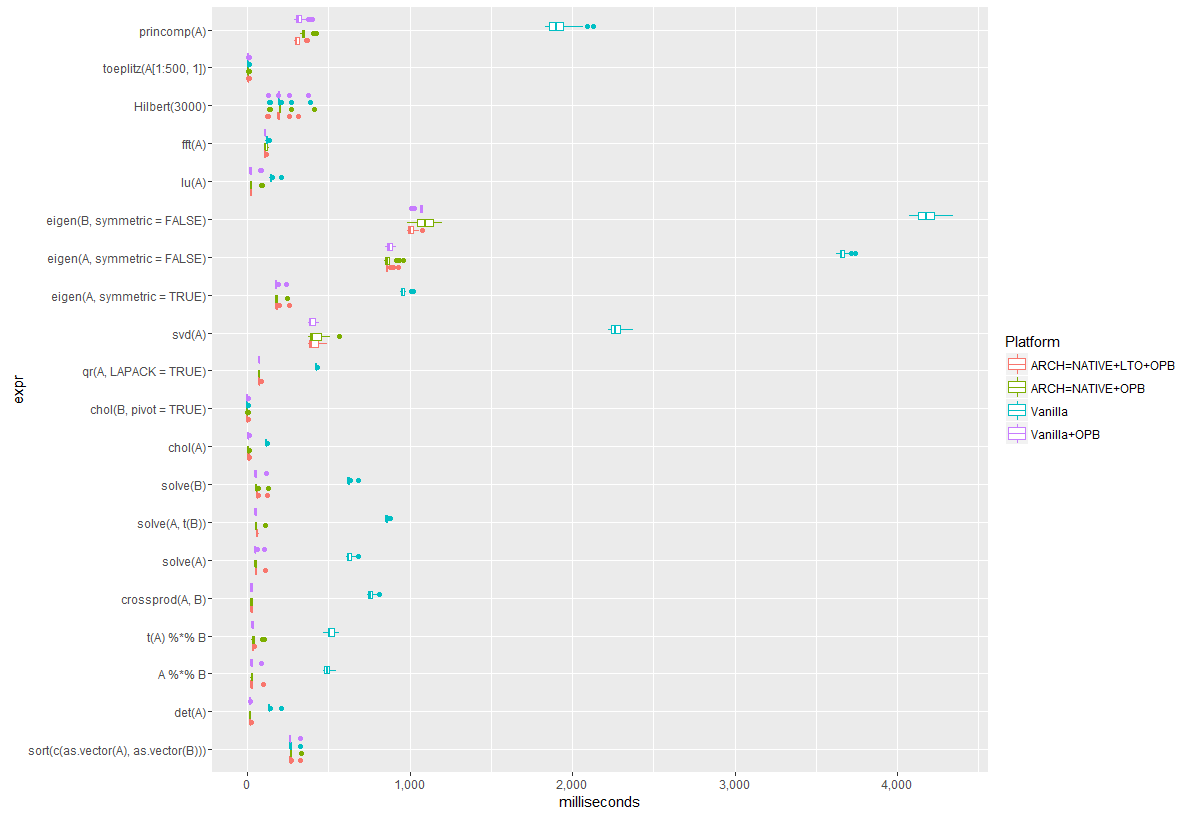
As there are only 25 samples for each function, a jitter plot may be a bit simpler:
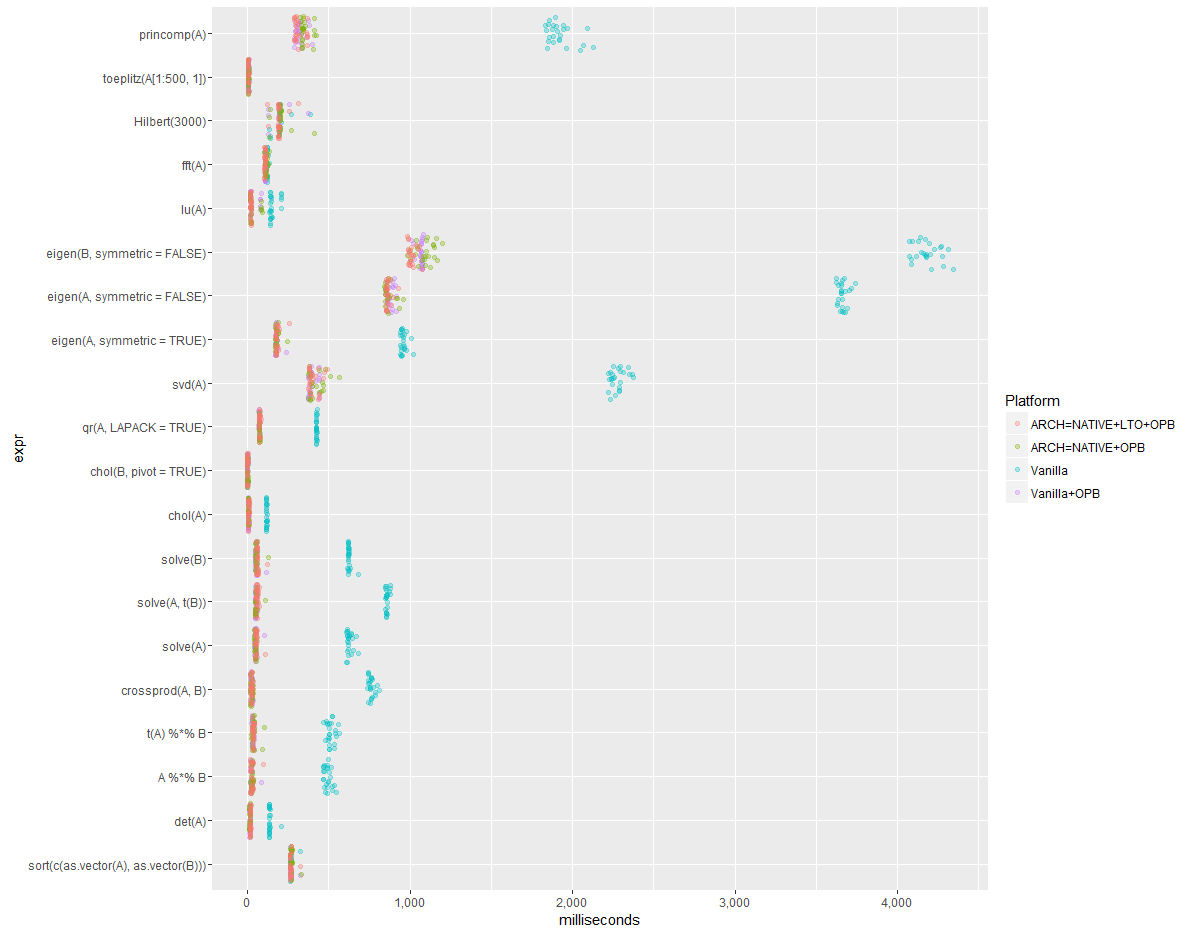
It is clear that just adding the BLAS makes a noticeable difference for matrix-related functionality. The other optimizations tend to provide some benefit, but nothing significant.
The non-BLAS related functions, understandably, don’t respond the same way to the BLAS. As I ran 5000 samples per expression, a jitter plot would not be that clear, even with a low alpha.
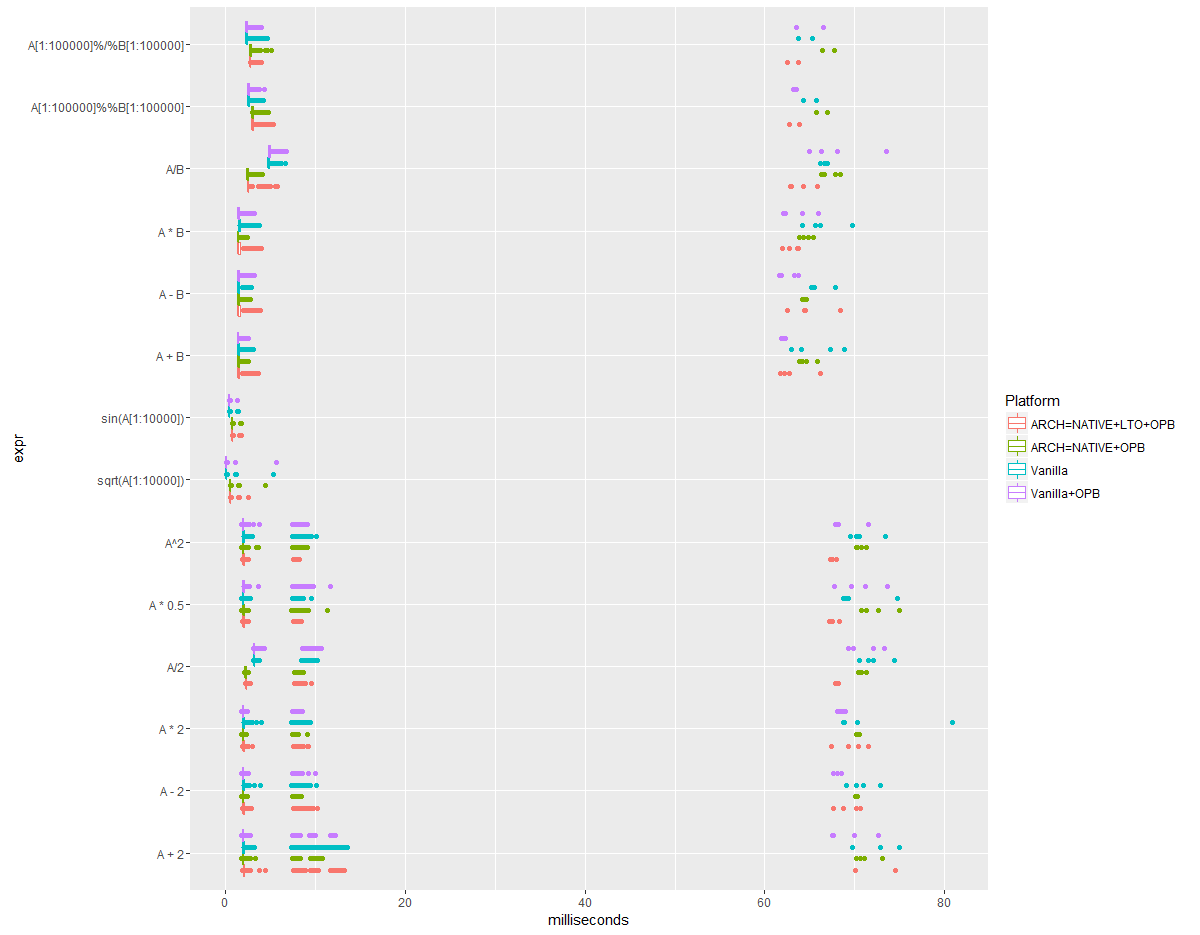
What is seen here, in my opinion, that using the local architecture sometimes improves performance, such as for division, and other retards it slightly, such as for sin and sqrt. I think the latter two depend on the optimization as well. Default R calls for -O3 for C code. The magnitude of the improvements seems to be greater than the change in those times where there is an impediment, at least when eyeballing the plot. If I recall from previous tests, strangely, it may be slightly more efficient to pass -mtune = native, at least for my test suite. I’m not sure why, as arch implies tune. I’d have to recompile R yet again to test it, though. Also, with 5000 iterations per expression, garbage collection has to be run on occasion, which accounts for those outlier points.
In summation, if you deal with heavy calculation in R, specifically matrix-related, you will notice significant speed improvement by replacing the vanilla Rblas.dll with a faster one. Compiling or tuning for a specific architecture may show some small increases, but does not return the same results.
While it’s actually easier now to compile OpenBLAS for R and in R on Windows, my instructions are a bit dated, and so I’ll have to update those eventually. I have considered hosting some pre-compiled Rblas files, as Dr. Ei-ji Nakama does, but I’ve held back for two reasons 1) I have to ensure I apply the proper licenses and 2) I’m a bit concerned about someone suing or the like if for whatever reason, a blas didn’t work properly. I have disclaimers and all, but you never know 8-).
In any event, I’m always interested in hearing comments about your experience with compiling R or a fast BLAS for Windows, and especially if you found any of my previous posts helpful. Thanks!
Raw Benchmark Output
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 |
R version 3.2.4 Revised (2016-03-16 r70336) (pure vanilla) Unit: milliseconds BLAS expr Min LQ Median UQ Max Mean SD CV n (fctr) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (int) 1 sort(c(as.vector(A), as.vector(B))) 264.56 266.56 267.13 270.50 327.81 270.39 12.15 0.04492 25 2 det(A) 134.83 135.77 136.47 137.74 206.93 139.83 14.12 0.10095 25 3 A %*% B 465.64 473.39 492.22 504.79 546.33 493.55 22.62 0.04583 25 4 t(A) %*% B 468.96 501.26 506.00 535.00 564.67 514.08 24.71 0.04807 25 5 crossprod(A, B) 737.52 746.47 759.38 768.71 813.29 762.19 18.66 0.02449 25 6 solve(A) 607.80 615.18 621.48 639.45 679.81 628.14 18.80 0.02992 25 7 solve(A, t(B)) 847.49 853.39 855.29 859.28 881.07 858.57 8.89 0.01036 25 8 solve(B) 617.06 621.25 622.45 624.65 683.30 625.33 12.56 0.02008 25 9 chol(A) 116.61 117.19 117.40 118.45 123.19 118.46 1.99 0.01676 25 10 chol(B, pivot = TRUE) 2.38 2.45 2.52 2.59 6.91 3.15 1.51 0.48091 25 11 qr(A, LAPACK = TRUE) 423.32 424.46 425.25 426.35 432.92 425.62 2.07 0.00487 25 12 svd(A) 2219.86 2242.51 2265.10 2294.88 2372.62 2277.14 45.47 0.01997 25 13 eigen(A, symmetric = TRUE) 939.63 946.36 952.16 963.85 1020.42 959.00 19.78 0.02063 25 14 eigen(A, symmetric = FALSE) 3623.95 3650.20 3657.46 3675.48 3740.09 3662.55 28.50 0.00778 25 15 eigen(B, symmetric = FALSE) 4072.00 4127.98 4175.12 4228.25 4344.13 4183.00 77.04 0.01842 25 16 lu(A) 137.73 142.06 144.51 147.26 210.54 156.60 26.47 0.16901 25 17 fft(A) 112.27 116.98 119.89 123.29 135.01 120.63 5.20 0.04308 25 18 Hilbert(3000) 134.83 196.37 197.50 199.45 386.30 201.86 46.23 0.22905 25 19 toeplitz(A[1:500, 1]) 4.92 5.06 5.09 5.45 10.49 5.80 1.72 0.29759 25 20 princomp(A) 1834.20 1855.31 1903.78 1947.02 2127.45 1923.42 81.44 0.04234 25 NotBLAS expr Min LQ Median UQ Max Mean SD CV n (fctr) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (int) 1 A + 2 1.719 1.891 1.922 2.012 74.96 2.542 2.5880 1.018 5000 2 A - 2 1.723 1.910 1.965 2.066 72.86 2.628 2.6389 1.004 5000 3 A * 2 1.725 1.900 1.948 2.049 80.89 2.604 2.6526 1.019 5000 4 A/2 3.014 3.162 3.179 3.205 74.44 3.776 2.5372 0.672 5000 5 A * 0.5 1.718 1.884 1.908 1.971 74.80 2.538 2.5780 1.016 5000 6 A^2 1.718 1.896 1.939 2.036 73.41 2.587 2.6111 1.009 5000 7 sqrt(A[1:10000]) 0.110 0.111 0.111 0.112 5.30 0.116 0.0833 0.717 5000 8 sin(A[1:10000]) 0.364 0.365 0.365 0.366 1.35 0.368 0.0429 0.117 5000 9 A + B 1.306 1.384 1.448 1.542 68.83 1.582 1.8367 1.161 5000 10 A - B 1.308 1.355 1.432 1.539 67.87 1.571 1.8412 1.172 5000 11 A * B 1.310 1.410 1.471 1.571 69.73 1.610 1.8548 1.152 5000 12 A/B 4.767 4.779 4.789 4.853 66.93 4.946 1.7605 0.356 5000 13 A[1:100000]%%B[1:100000] 2.528 2.544 2.558 2.583 65.80 2.639 1.2633 0.479 5000 14 A[1:100000]%/%B[1:100000] 2.271 2.296 2.318 2.370 65.33 2.423 1.2646 0.522 5000 ---------- R version 3.2.4 Revised (2016-03-16 r70336) (pure vanilla) With SandyBridge-specific OpenBLAS (2.17) Unit: milliseconds BLAS expr Min LQ Median UQ Max Mean SD CV n (fctr) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (int) 1 sort(c(as.vector(A), as.vector(B))) 264.10 265.06 265.77 266.93 323.4 268.39 11.52 0.0429 25 2 det(A) 14.31 14.57 15.26 16.67 20.0 15.82 1.43 0.0903 25 3 A %*% B 19.25 21.34 26.83 28.49 84.1 27.78 12.68 0.4563 25 4 t(A) %*% B 26.46 30.04 32.20 38.76 43.6 34.25 5.37 0.1567 25 5 crossprod(A, B) 17.63 21.14 22.82 27.48 35.5 24.68 5.10 0.2066 25 6 solve(A) 40.67 45.92 49.58 51.48 107.1 51.29 12.37 0.2412 25 7 solve(A, t(B)) 46.32 50.88 51.63 56.40 63.2 53.00 4.24 0.0799 25 8 solve(B) 47.09 51.22 51.72 56.44 118.6 56.32 13.71 0.2435 25 9 chol(A) 6.59 6.65 6.77 7.01 10.6 7.38 1.39 0.1890 25 10 chol(B, pivot = TRUE) 2.36 2.47 2.50 2.58 6.8 3.25 1.58 0.4851 25 11 qr(A, LAPACK = TRUE) 70.19 71.59 72.47 74.69 79.1 72.96 2.22 0.0304 25 12 svd(A) 375.74 378.56 389.32 415.33 444.7 399.66 26.19 0.0655 25 13 eigen(A, symmetric = TRUE) 171.72 175.04 176.94 177.97 239.8 179.80 13.20 0.0734 25 14 eigen(A, symmetric = FALSE) 849.09 859.77 872.76 891.57 915.7 876.86 20.89 0.0238 25 15 eigen(B, symmetric = FALSE) 1011.80 1065.85 1070.08 1075.52 1085.1 1065.76 18.14 0.0170 25 16 lu(A) 17.91 18.91 20.78 22.62 82.8 32.68 25.43 0.7782 25 17 fft(A) 110.52 111.17 113.16 113.34 113.8 112.33 1.18 0.0105 25 18 Hilbert(3000) 128.99 194.32 194.70 195.01 377.4 196.80 45.44 0.2309 25 19 toeplitz(A[1:500, 1]) 4.77 4.96 5.03 5.04 10.0 5.58 1.64 0.2937 25 20 princomp(A) 285.96 302.37 316.33 329.08 400.5 322.00 29.13 0.0905 25 NotBLAS expr Min LQ Median UQ Max Mean SD CV n (fctr) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (int) 1 A + 2 1.712 1.887 1.904 1.938 72.64 2.514 2.6240 1.044 5000 2 A - 2 1.723 1.893 1.913 1.962 68.52 2.540 2.5268 0.995 5000 3 A * 2 1.721 1.894 1.918 1.974 68.97 2.543 2.5326 0.996 5000 4 A/2 3.016 3.173 3.192 3.229 73.36 3.804 2.5315 0.665 5000 5 A * 0.5 1.724 1.900 1.939 2.049 73.70 2.590 2.6048 1.006 5000 6 A^2 1.722 1.890 1.910 1.974 71.55 2.543 2.5479 1.002 5000 7 sqrt(A[1:10000]) 0.110 0.111 0.111 0.112 5.59 0.116 0.0876 0.753 5000 8 sin(A[1:10000]) 0.364 0.365 0.366 0.366 1.32 0.370 0.0408 0.110 5000 9 A + B 1.310 1.336 1.378 1.447 62.35 1.512 1.7318 1.146 5000 10 A - B 1.310 1.345 1.411 1.491 63.70 1.542 1.7465 1.133 5000 11 A * B 1.312 1.349 1.421 1.501 65.96 1.550 1.7753 1.145 5000 12 A/B 4.766 4.781 4.804 4.959 73.53 4.992 1.8146 0.364 5000 13 A[1:100000]%%B[1:100000] 2.526 2.541 2.550 2.591 63.56 2.638 1.2305 0.467 5000 14 A[1:100000]%/%B[1:100000] 2.272 2.294 2.310 2.361 66.49 2.399 1.2681 0.529 5000 ---------- R version 3.2.4 Patched (2016-03-28 r70390) -- "Very Secure Dishes" Compiled with -march=native With SandyBridge-specific OpenBLAS (2.17) BLAS expr Min LQ Median UQ Max Mean SD CV n (fctr) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (int) 1 sort(c(as.vector(A), as.vector(B))) 266.79 267.24 268.46 271.46 329.37 272.04 12.36 0.0454 25 2 det(A) 14.24 14.43 15.12 16.94 18.63 15.69 1.43 0.0911 25 3 A %*% B 20.95 24.25 28.79 31.89 34.96 28.26 4.21 0.1490 25 4 t(A) %*% B 26.70 29.53 33.74 41.83 103.68 39.71 18.48 0.4652 25 5 crossprod(A, B) 17.65 19.46 28.94 31.99 36.97 26.53 6.56 0.2474 25 6 solve(A) 41.47 45.97 49.44 52.75 56.85 49.38 4.19 0.0849 25 7 solve(A, t(B)) 46.34 51.00 53.22 55.86 113.34 55.53 12.45 0.2242 25 8 solve(B) 47.90 52.74 54.88 57.05 126.30 58.01 15.05 0.2595 25 9 chol(A) 6.57 6.72 6.93 7.43 12.90 7.74 1.84 0.2377 25 10 chol(B, pivot = TRUE) 2.37 2.47 2.49 2.53 6.26 3.22 1.53 0.4755 25 11 qr(A, LAPACK = TRUE) 70.84 71.54 73.10 74.91 78.28 73.59 2.19 0.0298 25 12 svd(A) 375.93 384.60 399.36 454.94 563.73 421.43 49.29 0.1170 25 13 eigen(A, symmetric = TRUE) 170.29 174.23 177.88 185.33 244.08 182.23 14.50 0.0796 25 14 eigen(A, symmetric = FALSE) 839.89 851.24 861.85 874.42 961.61 870.93 31.10 0.0357 25 15 eigen(B, symmetric = FALSE) 985.55 1045.25 1097.99 1142.28 1200.26 1093.09 56.17 0.0514 25 16 lu(A) 18.25 20.03 21.52 23.14 91.58 34.15 27.10 0.7936 25 17 fft(A) 106.88 110.80 112.50 119.96 132.55 115.51 6.66 0.0576 25 18 Hilbert(3000) 133.10 197.69 201.83 204.57 411.96 205.26 50.69 0.2470 25 19 toeplitz(A[1:500, 1]) 5.04 5.20 5.35 5.49 10.66 5.94 1.65 0.2773 25 20 princomp(A) 326.08 336.14 341.65 349.99 425.50 354.56 31.37 0.0885 25 NotBLAS expr Min LQ Median UQ Max Mean SD CV n (fctr) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (int) 1 A + 2 1.731 1.890 1.911 1.956 73.12 2.538 2.6108 1.0286 5000 2 A - 2 1.726 1.884 1.903 1.943 70.36 2.527 2.5691 1.0168 5000 3 A * 2 1.727 1.891 1.910 1.945 70.49 2.531 2.5708 1.0156 5000 4 A/2 2.040 2.193 2.210 2.236 71.35 2.816 2.5552 0.9075 5000 5 A * 0.5 1.726 1.902 1.939 2.016 74.95 2.591 2.6501 1.0227 5000 6 A^2 1.727 1.886 1.907 1.966 71.32 2.541 2.5889 1.0188 5000 7 sqrt(A[1:10000]) 0.509 0.516 0.516 0.517 4.36 0.521 0.0670 0.1285 5000 8 sin(A[1:10000]) 0.715 0.720 0.721 0.722 1.72 0.725 0.0416 0.0573 5000 9 A + B 1.331 1.356 1.378 1.459 65.85 1.522 1.8010 1.1831 5000 10 A - B 1.331 1.357 1.383 1.461 64.68 1.527 1.7970 1.1765 5000 11 A * B 1.332 1.354 1.372 1.431 65.46 1.513 1.8009 1.1905 5000 12 A/B 2.412 2.423 2.432 2.460 68.39 2.580 1.8492 0.7168 5000 13 A[1:100000]%%B[1:100000] 2.917 2.999 3.005 3.027 67.03 3.084 1.2797 0.4150 5000 14 A[1:100000]%/%B[1:100000] 2.683 2.759 2.769 2.816 67.74 2.861 1.2999 0.4543 5000 ---------- R version 3.2.4 Patched (2016-03-28 r70390) -- "Very Secure Dishes" Compiled with -march=native and partial LTO (R core, blas, and lapack only) With SandyBridge-specific OpenBLAS (2.17) BLAS expr Min LQ Median UQ Max Mean SD CV n (fctr) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (int) 1 sort(c(as.vector(A), as.vector(B))) 263.84 265.83 266.39 268.22 323.52 269.49 11.48 0.0426 25 2 det(A) 16.55 17.15 17.72 19.73 23.69 18.55 1.82 0.0982 25 3 A %*% B 19.55 21.52 25.02 33.33 96.59 29.20 15.17 0.5195 25 4 t(A) %*% B 27.71 33.26 35.59 38.03 45.20 35.47 4.33 0.1220 25 5 crossprod(A, B) 17.81 21.49 25.98 28.99 34.36 25.94 4.49 0.1730 25 6 solve(A) 48.38 51.94 54.40 57.04 112.31 56.72 12.03 0.2122 25 7 solve(A, t(B)) 54.93 56.65 60.59 63.24 72.91 61.05 5.25 0.0859 25 8 solve(B) 55.50 58.85 60.88 62.99 121.31 63.46 12.50 0.1969 25 9 chol(A) 8.57 8.69 8.80 8.98 12.21 9.40 1.28 0.1361 25 10 chol(B, pivot = TRUE) 2.35 2.44 2.51 2.62 6.87 3.18 1.60 0.5035 25 11 qr(A, LAPACK = TRUE) 71.16 72.38 73.57 74.85 83.43 74.41 2.93 0.0393 25 12 svd(A) 376.02 380.71 392.98 437.93 490.97 407.28 34.08 0.0837 25 13 eigen(A, symmetric = TRUE) 173.96 176.57 179.35 181.38 259.73 183.29 16.79 0.0916 25 14 eigen(A, symmetric = FALSE) 852.68 856.26 860.10 864.31 926.66 865.16 16.63 0.0192 25 15 eigen(B, symmetric = FALSE) 987.24 993.14 1001.10 1020.62 1079.71 1010.79 24.32 0.0241 25 16 lu(A) 19.18 20.01 21.76 24.21 26.51 22.11 2.44 0.1103 25 17 fft(A) 106.65 107.09 108.58 110.35 116.92 108.98 2.36 0.0216 25 18 Hilbert(3000) 125.60 191.73 192.18 194.44 314.63 195.15 33.81 0.1732 25 19 toeplitz(A[1:500, 1]) 4.99 5.18 5.21 5.24 10.22 5.79 1.62 0.2801 25 20 princomp(A) 285.97 296.12 300.58 317.75 370.74 315.50 30.97 0.0982 25 NotBLAS expr Min LQ Median UQ Max Mean SD CV n (fctr) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (dbl) (int) 1 A + 2 1.828 1.995 2.022 2.091 74.52 2.615 2.4756 0.9468 5000 2 A - 2 1.807 1.973 1.995 2.064 70.60 2.636 2.5624 0.9721 5000 3 A * 2 1.827 1.991 2.009 2.054 71.57 2.637 2.5618 0.9714 5000 4 A/2 2.147 2.293 2.309 2.335 68.18 2.912 2.4859 0.8537 5000 5 A * 0.5 1.817 1.990 2.007 2.049 68.35 2.628 2.5134 0.9564 5000 6 A^2 1.795 1.964 1.980 2.011 67.96 2.596 2.5082 0.9660 5000 7 sqrt(A[1:10000]) 0.531 0.535 0.536 0.536 2.51 0.540 0.0474 0.0878 5000 8 sin(A[1:10000]) 0.719 0.726 0.726 0.727 1.70 0.728 0.0413 0.0566 5000 9 A + B 1.326 1.355 1.391 1.545 66.25 1.690 1.8104 1.0713 5000 10 A - B 1.321 1.365 1.437 1.602 68.45 1.726 1.8618 1.0788 5000 11 A * B 1.327 1.366 1.439 1.586 63.71 1.719 1.8044 1.0499 5000 12 A/B 2.435 2.463 2.530 2.560 65.87 2.804 1.8057 0.6439 5000 13 A[1:100000]%%B[1:100000] 2.987 3.002 3.007 3.025 63.89 3.092 1.2231 0.3956 5000 14 A[1:100000]%/%B[1:100000] 2.718 2.732 2.736 2.745 63.70 2.809 1.2202 0.4344 5000 |

[…] article was first published on R – Strange Attractors, and kindly contributed to […]
Hello.
What’s the difference between using your method (replacing openblas dll) vs using R Open from here https://mran.revolutionanalytics.com/rro/#intelmkl1 ?
Not much. I started before there was MS R, and the MKL was not available for use for commercial purposes, which is why I was originally restricted to ATLAS, Goto, and eventually OpenBLAS. Also, the OpenBLAS project has some studies showing OPB as fast if not faster than MKL, but I’ve never compared the two after building R. Since I maintain some packages for R on Windows, I need to be able to compile, so I’ve gotten used to building R from source. By all means, try them both and see which works better for you!
I compiled on i7 4790 (haswell) using -mtune=native , 64bit R.
compared with original R, my Blas is about 10 times faster. NotBlas functions differs, A/B is like 3 times faster, simple calc is around 5% to 10% or no significant improvement. Overall, well done!
have you compiled for 32bit as well? thanks.
Hi, @Ricky, thank you very much and sorry about the delay. Yes, I used to compile ATLAS for 32bit, as a matter of fact, the two latest entries at https://cran.r-project.org/bin/windows/contrib/ATLAS/ (C2D and C2i7) are my contributions. However, once I switched to a 64 bit operating system, I had severe issues compiling ATLAS, which is why I switched to OpenBLAS.